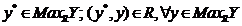10. Описание предпочтений на языке бинарных отношений.

Отдельный исход сам по себе не оценивается, критериальные функции не вводятся.

Каждая пара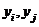  может находиться в одном из следующих отношений:

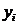•   предпочтительнее 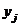(строгий порядок) .
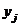•  предпочтительнее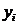 
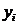•  не менее предпочтителен, чем  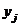(квазипорядок).
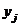•  не менее предпочтителен, чем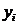 
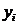•  эквивалентен .

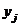Постановка задачи выбора на языке бинарных отношений.

Пусть Y - множество исходов, R - произвольное бинарное отношение на Y, тогда пара <Y,R>  называется моделью выбора.

Пусть задана модель выбора <Y,R>, элемент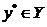 называетсянаилучшим по R в Y, если  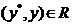при.

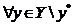Пусть задана модель выбора <Y,R>, элемент называетсямаксимальным по R вY, если.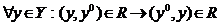

Обозначим множество максимальных элементов в <Y,R> как.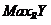

Множество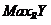называется внешне устойчивым, если для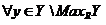найдется такой , чтосправедливо

Если множество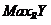 является внешне устойчивым, то последующий выбор оптимального элемента проводится только в пределах этого множества.

Внешне устойчивое множество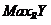называется ядром отношений в.

Задача принятия решений на языке бинарных отношений R в Y.