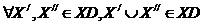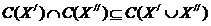11. Функция выбора
Выделение из множества альтернатив подмножества “лучших” вариантов (А не оценка каждой альтернативы с помощью одного или нескольких числовых критериев и не попарное сравнение альтернатив по предпочтительности).
Определение функции выбора.
Пусть A- множество всех возможных альтернатив, тогда 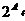 - множество всех подмножеств A.
- множество всех подмножеств A. 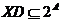 - множество допустимых предъявлений.
- множество допустимых предъявлений.
Функцией выбора называется отображение 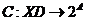
такое, что для любого множества 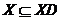
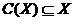
Функция выбора – отображение, определяющее зависимость выбора от предъявления 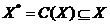
| Способы задания функций выбора | ||
| Таблица | Набор свойств | Механизм выбора |
Примеры функций выбора
Скалярный оптимизационный механизм:
Выбор лучшего по заданному скалярному критерию качества f(X) варианта 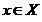
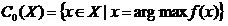
Оптимизационный механизм доминирования:
Выбор лучшего варианта в соответствии с бинарным отношением доминирования 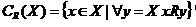
Механизм ограничений:
Выбор элементов x, “лучших” по R фиксированного элемента 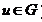
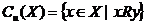 Турнирный механизм, определяемый бинарным отношением :
Турнирный механизм, определяемый бинарным отношением :
Скалярный оптимизационный механизм с критерием 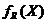 , специальным образом зависящим от R,
, специальным образом зависящим от R, 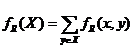 , где:
, где: 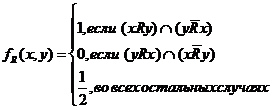
Свойства функции выбора.
Наследование:
Вариант, выбираемый из некоторого множества, будет также выбран, если предъявить для выбора любое подмножество, содержащее этот вариант .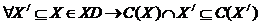
Отбрасывание:
Если удалить из предъявляемого множества какие-то невыбранные альтернативы, то выбор на оставшемся множестве не изменится (Независимость от отвергнутых альтернатив). 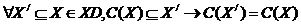
Согласованность:
Если вариант выбирается в каждом из двух множеств (предъявлений), то он будет выбран и в объединении этих множеств