12. Общая характеристика линейных задач скалярной оптимизации
Задачи условной оптимизации.
Линейные задачи являются элементом более широкого класса задач – задач принятия решений при наличии ограничений, которые называются задачами условной оптимизации.
Задачи условной оптимизации призваны так распределить ограниченные ресурсы, чтобы максимизировать или минимизировать критерий эффективности.
Критерий эффективность, который при принятии решения требуется оптимизировать, в задачах условной оптимизации называется целевой функцией.
Свойства задач линейной оптимизации.
1. В каждой задаче линейной оптимизации существует единственный критерий эффективности, который необходимо максимизировать или минимизировать.
2. В задачах линейной оптимизации обязательно присутствуют ограничения, которые и определяют наличие максимума (минимума) целевой функции.
3. Целевая функция и ограничения имеют характер линейных зависимостей.
Общая задача линейного программирования.
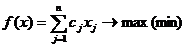 , при следующих ограничениях:
, при следующих ограничениях:


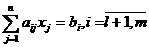
 с-j, a-ij, b-i - заданные вещественные числа; k, l, m, n- целые числа.
с-j, a-ij, b-i - заданные вещественные числа; k, l, m, n- целые числа.
Вектор  , удовлетворяющий ограничениям задачи ЛП, называется допустимым решением (планом).
, удовлетворяющий ограничениям задачи ЛП, называется допустимым решением (планом).
Допустимое решение 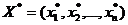 , при котором целевая функция задачи ЛП принимает максимальное (минимальное) значение, называется оптимальным решением (планом).
, при котором целевая функция задачи ЛП принимает максимальное (минимальное) значение, называется оптимальным решением (планом).
Задача линейного программирования в матричной форме.
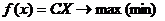 при следующих ограничениях:
при следующих ограничениях:  , X- вектор переменных размерности 1*n, C - вектор оценок задачи ЛП размерности 1*n, A - матрица размерности m*n, B- вектор ресурсов размерности m*1.
, X- вектор переменных размерности 1*n, C - вектор оценок задачи ЛП размерности 1*n, A - матрица размерности m*n, B- вектор ресурсов размерности m*1.
Типы задач линейного программирования.
1. A- множество типов изделий, выпускаемых на данном предприятии, c-i - прибыль от выпуска одного изделия, x-i - количество изделий i-го типа. Целевая функция выражается в векторной форме: .
.
2. A- множество типов изделий, B - множество технологий, c-i,j - прибыль от выпуска одного изделия i-го типа по технологии (i принадлежит A) , j - количество изделий(j принадлежит B). Целевая функция выражается в матричной форме:  .
.
3. A - пункты отправления, B - пункты назначения, c-ij- цена доставки единицы продукции из i-го пункта отправления (принадлежит A) в j-й пункт назначения (принадлежит B), x-ij- количество единиц продукции. Целевая функция выражается в матричной форме:  .
.
4.A- выполняемые работы, B- исполнители, c-ij - показатель эффективности выполнения i-ой работы (прин. А) j-м исполнителем (прин.B), x-ij- параметр назначения (x-ij=1 если на i-ю работу назначается j-й исполнитель, x-ij=0 в обратном случае). Целевая функция выражается в матричной форме: 
Методы решения задач линейного программирования.
| Тип задачи | Название задачи | Методы решения |
| 1 | Задачи общего вида | Универсальные методы |
| 2 | Задача распределенного общего вида | Универсальные методы |
| 3 | Транспортная задача | Универсальные (специальные) методы |
| 4 | Задача о назначениях | Универсальные (специальные) методы |
Условия представления задач предметной области в виде задач линейного программирования.
1. Делимость. Все показатели производственно-технологического процесса могут быть увеличены или уменьшены при сохранении их взаимной пропорциональности.
2. Аддитивность. Полное количество каждого из потребленных ресурсов равняется сумме одноименных ресурсов, затраченных при реализации всех применявшихся технологических процессов.
Применительно к фиксированному производственно-технологическому процессу приведенные условия означают, что доходы строго пропорциональны затраченным ресурсам, а непропорциональный эффект (технологического или экономического характера) оказывается невозможным.