15. Математическая модель транспортной задачи
В m пунктах отправления 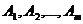 (будем называть их поставщиками) находится
(будем называть их поставщиками) находится 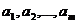 соответственно единиц однородного груза (ресурсов), который должен быть доставлен n потребителям
соответственно единиц однородного груза (ресурсов), который должен быть доставлен n потребителям  в количествах
в количествах 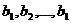 единиц соответственно (назовем их потребностями). Известны транспортные издержки c-ij (расходы), связанные с перевозкой единицы груза из пункта отправления i в пункт потребления j. Требуется спланировать перевозки (указать, сколько единиц груза должно быть отправлено от поставщика потребителю x-ij) так, чтобы:
единиц соответственно (назовем их потребностями). Известны транспортные издержки c-ij (расходы), связанные с перевозкой единицы груза из пункта отправления i в пункт потребления j. Требуется спланировать перевозки (указать, сколько единиц груза должно быть отправлено от поставщика потребителю x-ij) так, чтобы:
1. Весь груз из пунктов отправления был вывезен.
2. Потребности каждого пункта потребления были полностью удовлетворены.
3. Суммарные издержки на перевозки были минимальными.
Транспортная таблица.
| Поставщик | Потребитель | Запас | ||
| B-l | B-n |
| ||
| A-l | X-ll,C-ll | X-ln,C-ln |
| a-l |
| B-m | X-lm,C-lm | X-mn,C-mn |
| a-m |
| Потребность | b-l | b-n |
|
|
Модель транспортной задачи.
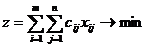 , при ограничениях:
, при ограничениях: 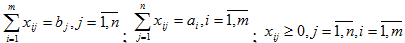 c-ij- матрица тарифов (издержек, транспортных расходов); x-ij- матрица перевозок.
c-ij- матрица тарифов (издержек, транспортных расходов); x-ij- матрица перевозок.
Особенности транспортной задачи.
Коэффициенты при переменных во всех уравнениях ограничений равны либо 0, либо 1.
Каждая переменная встречается только в двух уравнениях ограничений: один раз в системе ограничений по запасам и один раз в системе ограничений по потребностям.
Система уравнений симметрична относительно всех переменных.
Условие баланса транспортной задачи.
Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы в пунктах отправления были равны потребностям в грузе в пунктах назначения 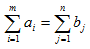 .
.
Если условие баланса выполняется, то модель транспортной задачи называется закрытой.
Если условие баланса не выполняется, то модель транспортной задачи называется открытой.
При нарушении баланса транспортной задачи.
Если 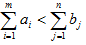 , в модель вводится фиктивный (m+1)-й поставщик
, в модель вводится фиктивный (m+1)-й поставщик 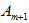 , для которого запас груза равен разности между суммарным спросом потребителей и фактическим запасом поставщиков
, для которого запас груза равен разности между суммарным спросом потребителей и фактическим запасом поставщиков 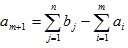 . Все тарифы на доставку груза от фиктивного поставщика считают равным 0:
. Все тарифы на доставку груза от фиктивного поставщика считают равным 0: 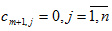 . В транспортную таблицу добавляется одна строка.
. В транспортную таблицу добавляется одна строка.
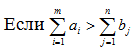 , в модель вводится фиктивный (n+1)-й потребитель
, в модель вводится фиктивный (n+1)-й потребитель 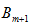 , для которого потребность равна разности между суммарным запасом поставщиков
, для которого потребность равна разности между суммарным запасом поставщиков 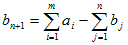 . Все тарифы на доставку груза с фиктивными потребностями считают равными 0:
. Все тарифы на доставку груза с фиктивными потребностями считают равными 0: 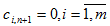 . В транспортную таблицу добавляется один столбец.
. В транспортную таблицу добавляется один столбец.