17. Математическая модель задачи о назначениях

Имеется n работ, которые нужно распределить между m исполнителями. Известны показатели эффективности выполнения i-м исполнителем j-ой работы c-ij . Требуется распределить работы между исполнителями так, чтобы:

1. Все работы были выполнены

2. Все исполнители были задействованы

3. Для выполнения каждой работы был использован только один исполнитель

4. Эффективность выполнения всего комплекса работ была максимальной (или затраты на выполнение комплекса были минимальными).   

Модель задачи о назначениях.

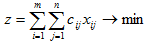 при ограничениях: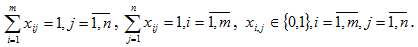 

Основные определения.

c-ij- матрица эффективности, x-ij - матрица назначений, z* - эффективность назначений (значение целевой функции, соответствующее оптимальному плану).

 Особенности задачи о назначениях.

В каждой строке и в каждом столбце матрицы 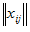 содержится ровно по одной единице.

Условие баланса 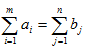 превращается в условие m=n.

В задаче m переменных равны 1, остальные равны 0.

При нарушении баланса задачи о назначениях.

Если n>m исключают некоторые работы (n-m). Например, наименее важные работы.

Если m>n исключают некоторых исполнителей (m-n). Например, наименее эффективных исполнителей.