19. Алгоритм решения задачи о назначениях венгерским методом

Задача на минимум:

Привести задачу к сбалансированному виду.

1. Записать условие задачи в виде матрицы эффективности.

2. В каждом столбце матрицы эффективности найти минимальный элемент 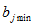 и вычесть его из элементов столбца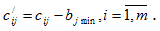 

3. В каждой строке матрицы эффективности найти минимальный элемент 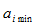 и вычесть его из элементов строки  .

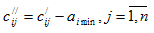4. Просматривая каждый столбец сверху вниз, отметить первый попавшийся нуль звездочкой 0* . При этом в одной строке не должно быть более одного 0* . Получилась система независимых нулей – начальный опорный план.

5. Проверить, равно ли число независимых нулей размерности задачи m. Если да – оптимальный план найден. Записать в матрицу назначений 1 в те места , которые соответствуют 0*. Если нет – перейти к п.7.

6. Отметить столбцы, содержащие независимые нули знаком “+”.

7. Среди невыделенных элементов (которые не помечены знаком “+”), найти минимальный элемент и обозначить его h . Если h=0 перейти к п.9, если нет – к п.11.

8. Проверить, есть ли в одной строке с h 0* . Если есть, то выделить нуль соответствующий h штрихом 0' . Выделить соответствующую строку знаком “+”, а выделение со столбца снять. Повторить п.8, если 0* нет, пометить  и перейти к п.10.

9. Построить цепочку, начиная с последнего 0', в которой будут чередоваться 0' и 0*. Причем, переход от 0' к 0* по столбцу, а 0* к 0' по  строке. Провести замену 0' на 0* и наоборот. Происходит увеличение числа независимых нулей на 1. Перейти к п.6.

10. Выполняется только после п.6 и предназначен для получения нулевых элементов путем преобразования матрицы эффективности. Вычесть H из всех невыделенных элементов (которые не относятся к выделенным столбцам и строкам) и прибавить h к элементам, находящимся на пересечении выделенных столбцов и строк. Перейти к п.6.

Задача на максимум:

1. Привести задачу к сбалансированному виду

2. Записать условия задачи в виде матрицы эффективности.

3. Преобразовать матрицу эффективности: Найти максимальный элемент матрицы и вычесть из него все элементы матрицы.

4. Решить задачу минимизации.