23. Задача о ранце, методы ее решения

Имеется ранец объемом b и дано множество предметов J . Для каждого предмета задана его ценность c-i и объем a-j. Необходимо найти такой набор предметов, который имел бы наибольшую ценность в походе при ограничении на суммарный объем.

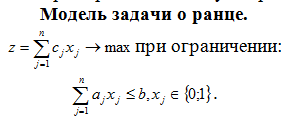 Решение задачи о ранце.

Подготовительный этап:

1. Для каждого предмета вычислить коэффициент 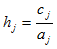, упорядочить и переименовать предметы в порядке убывания h-j.

2. Сформировать множество Go всех решений задачи и определить верхнюю оценку как 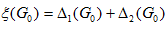. Для нахождения  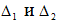определить такой номер l в нумерации предметов, для которого выполняется ограничение: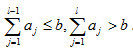 

Первая итерация:

1. Разделить исходное множество  на два непересекающихся подмножества 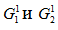. Для этого определить переменную, которая должна быть включена в оптимальное решение, исходя из условия 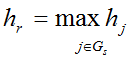, где G-s - это множество предметов, включение которых не приведет к нарушению ограничения.

2. Пусть r=1 тогда 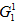 - это множество предметов, которое предполагает обязательное включение первого предмета в набор,  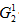- это множество решений в котором первый предмет не включается в набор.

3. Определить верхнюю оценку подмножества .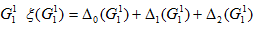

4. Определить верхнюю оценку подмножества .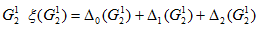

5. Сравнить оценки и выбрать наиболее перспективное подмножество.

Вторая итерация: Продолжаем делить множество на подмножество и т.д.

Условие окончания ветвления:

Если не существует такого номера, для которого не выполнялись бы ограничения, то процесс ветвления для этой вершины заканчивается, фиксируется ее максимальная верхняя оценка, совпадающая со значением критерия для этой вершины: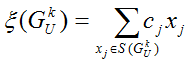 

Если эта верхняя оценка больше или равна значениям верхних оценок для других ранее отброшенных подмножеств, то задача о ранце считается решенной, и выполнение алгоритма заканчивается. В противном случае ветвлению подвергают ранее отброшенные вершины.