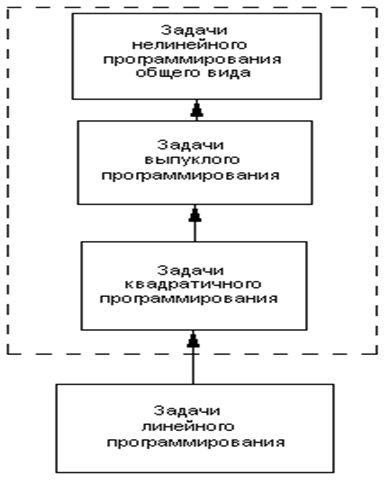
26. Виды задач нелинейного программирования.
Количество экстремумов целевой функции | |
Одноэкстремальные задачи
| Многоэкстремальные задачи |
Количество переменных | |
Однопараметрические задачи | Многопараметрические задачи |
Наличие ограничений | |
Задачи без ограничений | Задачи с ограничениями |
Задачи безусловной оптимизации | Задачи условной оптимизации |
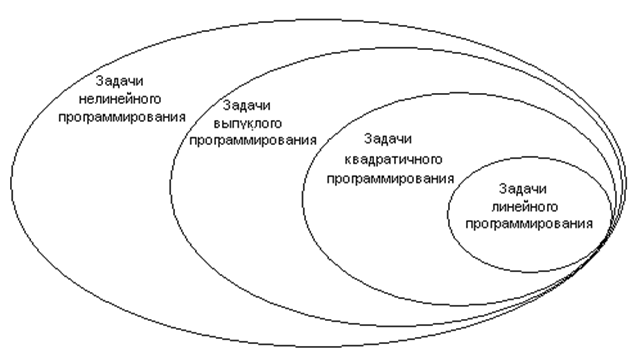
Выпуклое множество точек.
Все возможные пары и отрезки, соединяющие эти пары, находятся внутри множества. Множество точек без “дыр” и “углублений”.
Выпуклые | Невыпуклые |
| |
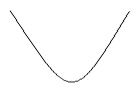
Выпуклая функция.
Функция f(x), определенная на выпуклом множестве {X} , называется выпуклой тогда и только тогда, когда для любых двух точек x1, x2, принадлежащих X и 0<= (лямбда) <=1 выполняется неравенство: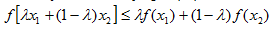
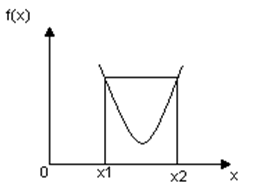
Отрезок, соединяющий любые две точки графика выпуклой функции, всегда проходит выше кривой в интервале между двумя этими точками.
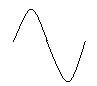
Отрезок, соединяющий любые две точки графика вогнутой функции, всегда проходит ниже кривой в интервале между двумя этими точками.
Если функции левых частей в ограничениях вида <= являются выпуклыми, а в ограничениях вида >= являются вогнутыми, то множество ограничений будет выпуклым множеством.
Выпуклая задача нелинейного программирования.
Задача минимизации с выпуклой целевой функцией и выпуклым множеством ограничений.
Вогнутая задача нелинейного программирования.
Задача максимизации с вогнутой целевой функцией и выпуклым множеством ограничений.
Вычислительная сложность задач нелинейного программирования.