28. Постановка задач многокритериального выбора

В задаче имеется несколько целевых функций. Каждая альтернатива должна удовлетворять нескольким противоречивым требованиям и характеризуется несколькими показателями.

Альтернативы имеют не скалярную, а векторную оценку:

 – задача векторной оптимизации.

Задача многокритериального выбора состоит в отыскании множества выбираемых решений  с учётом отношения предпочтения R , на основе векторного критерия 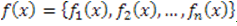 , отражающего цели ЛПР.

Пример: покупка цифрового фотоаппарата.

Цель – купить фотоаппарат наилучшего качества за минимальную цену: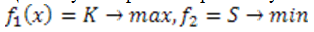

Типы многокритериальных задач.

• Задачи оптимизации на множестве целей, каждая из которых должна быть учтена при выборе  оптимального решения.
• Задачи оптимизации на множестве объектов, качество функционирования каждого из которых оценивается самостоятельным критерием.
• Задачи оптимизации на множестве условий функционирования. В задачах такого типа задан спектр условий, в которых предстоит работать объекту, и применительно к каждому условию качество функционирования оценивается самостоятельным критерием.
• Задачи оптимизации на множестве этапов функционирования. Рассматривается функционирование объекта на некотором интервале времени, разбитом  на несколько этапов, на кажом этапе, качество функционирования оценивается самостоятельным критерием.

Основные проблемы при решении многокритериальных задач.

1. Проблема выбора принципа оптимальности связана с определением свойств оптимального решения и решением вопроса – в каком смысле оптимальное решение превосходит все остальные.

2. Проблема нормализации возникает в связи с тем, что критерии имеют, как правило, различные единицы и масштабы измерения, и это делает невозможным их непосредственное сравнение. Операция приведения критериев к единому масштабу и безразмерному виду называется нормированием. Наиболее распространённым способом нормирования является замена абсолютных значений критериев их относительными велечинами.

3. Проблема учёта приоритета критериев возникает, если локальные критерии имеют различную значимость. Необходимо найти математическое определение приоритета и степень его влияния на решение задачи.

Требования к системе показателей (критериев).

Смысл каждого показателя должен определяться целью функционирования исследуемой системы.

В систему включаются показатели, не выводимые друг из друга простым математическим преобразованием. Они должны  быть основаны на независимых  или слабо коррелируемых характеристиках системы.

Каждый показатель должен нести  в себе какую-то новую  информацию о системе.

Система показателей эффективности должна давать всестороннюю и достоверную характеристику системы с полнотой, определяемой целями исследования.