29. Парето-оптимальность

Понятие Парето-оптимального множества.

Определение: альтернатива А называется доминирующей по отношению к альтернативе В, если по всем критериям оценки альтернативы А не хуже, чем альтернативы В, а хотя бы по одному критерию оценка А лучше. Альтернатива В при этом называется доминируемой.

Отношение Парето:

Если для некоторой точки  не существует более предпочтительной по Парето точки, т.е. такой точки y, что , то тогда точка 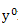 называется эффективным или Парето-оптимальным решением многокритериальной задачи (относится к множеству Парето).

Пример: понятие Парето-оптимального множества.

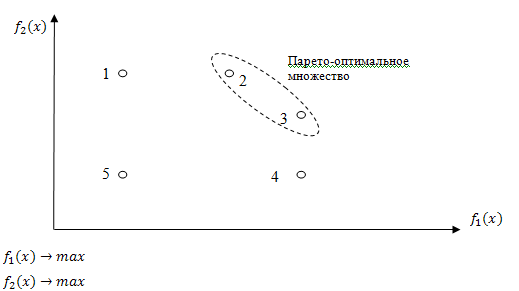
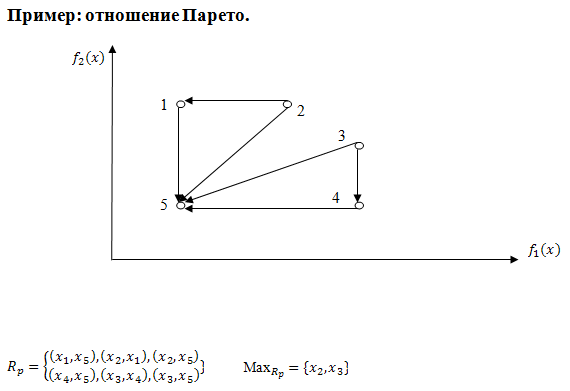
Aльтернатива является Парето-оптимальной, если она лучше других по какому-то из критериев.

Альтернативы, принадлежащие к множеству Парето, называются несравнимыми. Их невозможно сравнить непосредственно на основе  критериальных оценок. Они не находятся в отношении доминирования.

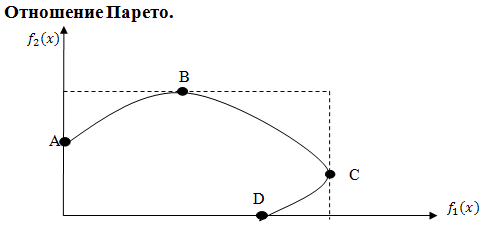
Аксиомы, являющиеся основой принципа Парето

Аксиома исключения доминирующих решений: Для всякой пары допустимых решений , для которых имеет место соотношение, выполнено.

Аксиома Парето: Для всех пар допустимых решений , для которых имеет место неравенство , выполняется соотношение.

Принцип Парето: наилучшее решение многокритериальной задачи всегда выбирается из Парето-оптимального множества.

Алгоритм нахождения множества Парето:

1. Принять P(Y)=Y, i=1, j=2. Создаётся текущее множество Парето-оптимальных векторов, которое  в начале совпадает с множеством Y.

2. Проверить выполнение неравенства .Если да, то перейти к п.3. Если нет, то перейти к п.5.

3. Удалить из текущего множества P(Y) вектор 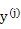, так как  он не является Парето-оптимальным. Перейти к п.4.

4. Проверить выполнение неравенства j<N. Если да, то положить на это болт  j=j+1 и вернуться к п.2. Если нет, то перейти к п.7.

5. Проверить выполнение неравенства . Если да, то перейти к п.6. Если нет, то перейти к п.4.

6. Удалить из текущего множества P(Y) вектор , так как он не является Парето-оптимальным. Перейти к п.7.

7. Проверить выполнение неравенства i<N-1. Если да, то положить i=i+1, j=j+1 И вернуться к п.2. Если нет, закончить вычисления.