42. Динамические задачи принятия решений.

Задачи управления проектами.

Проект – некоторое мероприятие с ограниченными ресурсами и сроками.

Характерным признаком проекта являются возможность его разбиения на ряд элементарных работ, которые выполняются независимо друг от друга. При этом можно выделить работы, выполнение которых не производиться, пока не выполнятся другие работы. Метод решения задач управления проектами – метод сетевого планирования.

В задачах сетевого планирования задаются:

• Наименование работ
• Трудоемкость работ
• Взаимная обусловленность работ, которая определяет после завершения какой работы (работ) можно начинать текущую.

Связь между работами графически представляется в виде сетевого графика.

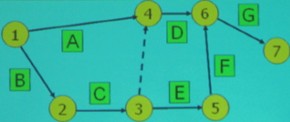
Типы задач оптимизации последовательности работ.

Обеспечить общую величину времени выполнения всего комплекса работ, не превышающую некоторого заданного значения. Методы решения подобных задач сводятся к манипулированию имеющимися ресурсами, с целью сокращения времени выполнения работ, находятся на критическом пути.

Минимизировать неравномерность использования ресурсов во времени при заданном сроке выполнения работ.

 Минимизировать расход ресурсов за весь период при нефиксированном сроке.

Задачи вариационного исчисления оптимального управления.

В основе постановки задач классического вариационного исчисления лежат физические процессы, которые, как правило, могут быть управляемы, т.е. могут осуществляться различными способами в зависимости от воли человека.

 Во всех вариантах таких задач речь идет о способе задания управления процессом. Требуется найти способ наилучшего в том или другом смысле управления, обеспечить минимизацию или максимизацию некоторой цели управления. При этом понятие “управление процессом” становится равноценно понятию “решение”.

 Развитие идей вариационного исчисления привело к созданию теории оптимального управления (ОУ).

ОУ - раздел математики, изучающий неклассические вариационные задачи. В отличие от классических вариационных задач, где управляющие параметры меняются в некоторой открытой области (без границы), теория ОУ охватывает и тот случай, когда управляющие параметры могут принимать и граничные значения. Последнее обстоятельство особенно существенно с прикладной точки зрения, поскольку при управлении техническим объектом именно положение “руля” “на упоре” часто обеспечивает оптимальное управление.

Центральным результатом теории ОУ является всемирно известный принцип максимума выдающегося математика Понтрягина, который на вербальном уровне можно сформулировать так: Для многих управляемых систем может быть построен такой процесс регулирования, при котором само состояние системы в каждый данный момент подсказывает наилучший с точки зрения всего процесса способ действий.

Принцип максимума Понтрягина определяет математические условия, необходимые для того, чтобы управление оказалось оптимальным, причем без предварительного определения оптимальной траектории, а путем последовательного регулирования данного процесса.

Этот результат и связанные с ним исследования, проведенные Понтрягиным и его сотрудниками, послужили исходным пунктам разработки теоретических, вычислительных, прикладных аспектов теории ОУ.

В общих чертах задача оптимального управления состоит в следующем. Рассматривается управляемый объект, под которым понимается некоторая машина, прибор или процесс, снабженные “рулями”. Манипулируя “рулями” (в пределах имеющихся ресурсов управления), мы определяем движение объекта, управляем им.

Возможности управлять объектом лимитируются не только ресурсами управления, но и тем, что в процессе движения объект не должен попадать в состояния, физически недоступные или недопустимые с точки зрения конкретных условий его эксплуатации.

Многоэтапные дискретные задачи.

Система (объект принятия решения) может находиться в дискретных состояниях. Число состояний конечно. Состояние и переход между ними могут быть представлены в виде графа.

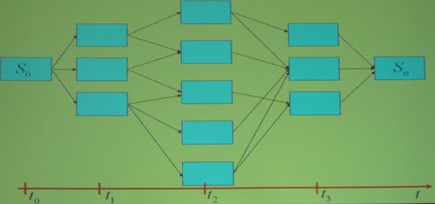
С каждой вершиной этого графа ассоциируется некоторой состояние, в котором находиться объект принятия решений. Дуги, выходящие из вершины, соответствуют возможным переходам из одного состояния в другое в зависимости от принимаемых решений.

Процесс развертывается во времени и движение по графу осуществляется слева направо. Каждая ветвь графа имеет свой вес – вещественное число, означающее соответствующие локальные затраты на переход в другое состояние.

Основная задача состоит в оптимальном выборе пути из начальной вершины в конечную. Оптимальность понимается в смысле построения допустимого пути, реализующего минимальные суммарные затраты (задача выбора минимального пути на графе).

В общем случае начальных и конечных вершин может быть несколько. 

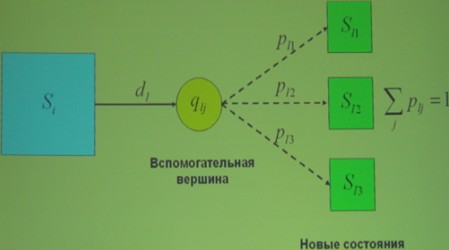
Детерминированная связь вершин.

Вероятностная связь вершин.