45. Сущность метода динамического программирования.
Метод динамического программирования.
Предназначен для задач, решение которых может быть представлено как некоторая многошаговая операция, т.е. последовательность однотипных шагов. Решение на любом шаге принимается с учетом результатов предыдущих шагов, а также с учетом последствий принимаемого решения для последующих шагов.
Общая постановка задачи динамического программирования.
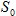- начальное состояние системы, 
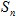- конечно состояние системы, U - допустимое управление системой (решение по управлению системы), Z - целевая функция 
.
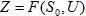Требуется определить допустимое управление системой U, приводящее систему из начального состояния 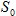в конечное 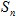, при котором Z достигает максимума или минимума.
Условия, которым должна удовлетворять задача, описываемая моделью динамического программирования
- Задача должна интерпретироваться, как n-шаговый процесс управления, а показатель эффективности процесса должен быть представлен в аддитивной форме, например, как сумма показателей эффективности на любом шаге.
- Структура задачи (или алгоритм решения) должна быть инвариантна относительно числа шагов n, т.е. должна быть определена для любого n и не зависеть от него.
- На каждом шаге состояние системы определяется конечным числом переменных состояния и управляется конечным числом переменных уравнения.
- Выбор управления на k-м шаге не влияет на предшествующие шаги, а состояние в начале этого шага есть функция только предшествующего состояния и выбранного на нем управления (отсутствия действия).
Некоторые задачи естественно распадаются на этапы, в других это деление приходится вводить искусственным путем.
Метод динамического программирования.
Динамическое программирование есть поэтапное планирование многошагового процесса, при котором на каждом этапе оптимизируется только один шаг. При этом управление на любом шаге должно выбираться с учетом всех его последствий в будущем.
Планируя многоэтапную операцию, необходимо выбирать управление на любом шаге, исходя не из более широких интересов операции в целом, и далеко не всегда эти две точки зрения совпадают.
Среди всех шагов существует один, который может планироваться попросту, “без оглядки на будущее”. Это последний шаг, он единственный из всех, который можно планировать так, что бы он как таковой приносил наибольшую выгоду.
Спланировав оптимальным образом этот последний шаг, можно к нему “пристраивать” предпоследний, к предпоследнему – еще один шаг и т.д.
Процесс динамического программирования всегда разворачивается в обратном по времени направлении: от конца к началу.
Принцип оптимальности Беллмана
Решение на любом шаге выбирается таким образом, чтобы обеспечить максимальную эффективность на данном шаге и на всех последовательных шагах
Основная вычислительная идея метода Беллмана
1. Решение задачи начинается с конца.
2. Исходная задача погружается во множество аналогичных задач с различными начальными вершинами и одной и той же конечной вершиной. При этом предполагается, что в качестве начальной вершины полностью выступает все без исключения вершины графа.
Порядок решения задач динамического программирования
Решение задач динамического программирования обычно включает два цикла
1. от последнего шага к первому (обратная прогонка, или условная оптимизация)
2. от первого шага к последнему (прямая прогонка, или безусловная оптимизация)
В цикле условной оптимизации для любого шага находится множество возможных состояний системы в начале данного шага. Для каждого из этих состояний находится условно оптимальное решение, т.е. решение оптимальное для данного состояния. Поиск условно оптимальных решений начинается с последнего шага.
В цикле безусловной оптимизации для каждого шага определяется безусловно оптимальное решение. Поиск безусловно оптимальных решений начинается с первого шага, т.к. для него известно начальное состояние.