47. Марковские модели принятия решений при конечном количестве этапов.

Анализируемая система или процесс характеризуются дискретным множеством состояний S={1,2…m}. Функционирование системы представляет собой логическую последовательность этапов 1,2…N . Общее количество этапов может быть либо фиксированным, либо равным бесконечности.  В момент времени t_n-1 система находится в одном из состояний S_i. ЛПР выбирает одну из стратегий z={1,2,…Z}, каждой стратегии соответствует матрица переходных вероятностей: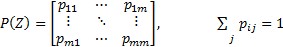 

Элемент матрицы p_ij (z) означает вероятность перехода системы из состояния S_i , в котором система находится в момент времени t_n-1 в состояние S_j в следующий момент времени t_n. Для каждой стратегии задана матрица D(z) = ||d_ij (z)||, элементы которой d_ij (z) определяют доход, который формируется системой при переходе из состояния S_i в S_j. Необходимо выбрать такую последовательность 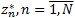, которая обеспечила бы максимальный доход от функционирования системы за N этапов.

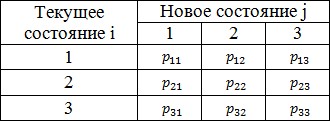
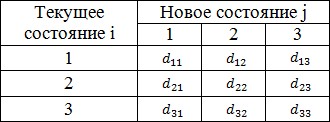
 Схема функционирования системы

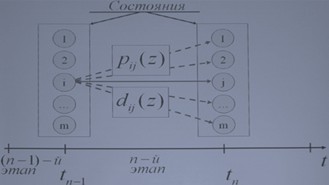
Процесс поведения системы называется марковским, если вероятность перехода системы в любое возможное состояние в каждый момент времени определяется только ее состоянием в предыдущий момент времени и не зависит от более ранней предыстории.

Применение метода динамического программирования для анализа марковской модели принятия решений: Введем функцию f_n(i)  - суммарный оптимальный доход для i-того состояния за  n-ый этап функционирования. Уравнение Беллмана можно представить следующим образом: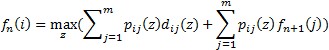  

Обозначим v_i(z) доход от пребывания системы в i-том состоянии при реализации решения z. Тогда 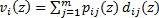, а уравнение Беллмана преобразуется к виду: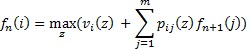 

Алгоритм анализа марковской модели принятия решения:

1. Решение задачи начинается с последнего этапа принятия решений n=N, 

2. Рассматривается принятие решений на предпоследнем этапе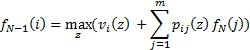 

3. Аналогично п.2 рассматривается принятие решений на других этапах до начального. Для каждого этапа выбирается максимальное значение дохода и фиксируется соответствующее оптимальное решение. Общее количество шагов равно количеству этапов.

4. Производится просмотр полученных результатов в прямом направлении и определяются безусловные оптимальные решения.