48. Марковские модели принятия решений при бесконечном количестве этапов.
Модификация базовой марковской модели принятия решений: количество этапов является бесконечным, и система при определенных ограничениях на матрицу переходных вероятностей переходит с течением времени в установившийся режим, а выбранная оптимальная стратегия не зависит от номера этапа. Стационарная стратегия – вектор, размерность которого равна числу состояний, а значение i-той компоненты соответствует номеру решения, которое целесообразно принимать в случае нахождения системы в состоянии i. Если число решений равно r, а число состояний – m, то количество стационарных стратегий определяется как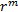 
.
Порядок формирования стационарных стратегий
Стратегия 1 предполагает, что при любом состоянии системы принимается решение 1, а в стратегия r – решение r.
Анализ модифицированной марковской модели принятия решений: анализ модифицированной марковской модели в установившемся режиме предполагает формирование для каждой стационарной стратегии матрицы переходных вероятностей P(u) и матрицы доходов D(u), вычисление векторов стационарного распределения вероятностей для каждой стратегии, определение доходов за один этап для каждой стратегии и выбор наилучшей из них.
Порядок конструирования матриц P(u) и D(u): первые строки матриц P(u) и D(u) соответствуют первым строкам матриц P(z = u1) и D(z = u1). Вторые строки матриц P(u) и D(u) соответствуют вторым строкам матриц P(z = u2) и D(z = u2), i-тые строки матриц P(u) и D(u) соответствуют i-тым строкам матриц P(z = ui) и D(z = ui).
Вычисление векторов стационарного распределения вероятностей: вычисляются для каждой стационарной стратегии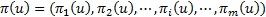 
Для нахождения вектора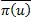 
используется система линейных уравнений, представленная в матричной форме 
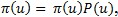совместно с условием нормировки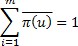 
Решение системы уравнений заключается в привидении её к виду Ax = B и дальнейшем применении стандартных процедур. Для привидения системы уравнений к требуемому виду необходимо транспонировать матрицу P(u), вычесть из неё единичную матрицу и заменить элементы первой строки на значения, равные единице. Вектор В содержит в первой позиции 1, а остальные значения равны 0.