62. Классификация игр. Характеристика игры.

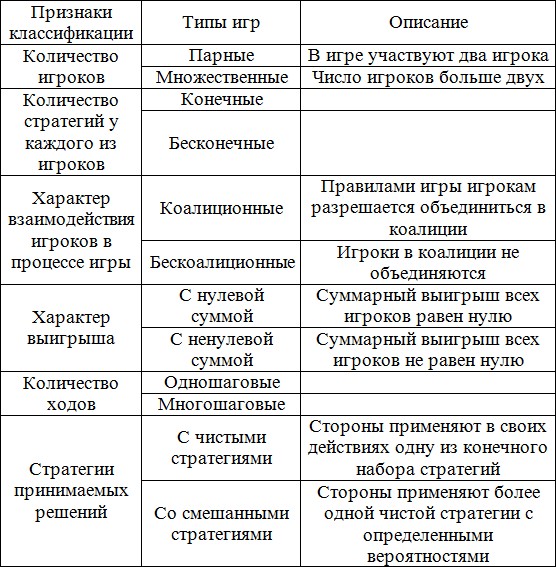
Характеристика игры.

Рассмотрим парную конечную бескоалиционную игру с нулевой суммой и чистыми стратегиями – базовый класс игр. Игроки A и B независимо друг от друга выбирают некоторые стратегии (альтернативы) a и b. В результате такого выбора складывается игровая ситуация (a,b), после этого игрок A получает выигрыш k(a,b), а игрок B столько же проигрывает. Поскольку число возможных действий каждого из игроков конечно, можно полагать, что 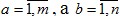. Тогда значения функции k(a,b) естественно представить в виде так называемой платежной матрицы:

Основной принцип теории игр – выбирай свое поведение так, чтобы оно было рассчитано на наихудший для тебя образ действий противника (принцип гарантированного результата).

Определение нижней цены игры.

Найти в каждой строке минимальное число .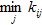

Выбрать максимальное из найденных чисел .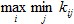

Определение верхней цены игры.

Найти в каждом столбце максимальное число .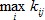

Выбрать минимальное из найденных чисел .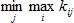

Оценка существования ситуации равновесия.

Найти в каждой строке минимальное число .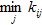

Выбрать максимальное из найденных чисел .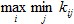

Найти в каждом столбце максимальное число .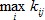

Выбрать минимальное из найденных чисел .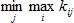

Выбирать стратегии можно случайным образом, но вероятности выбора стратегий должны определяться разумно.

Смешанная стратегия.

Смешная стратегия игрока – это вероятностное распределение на множестве чистых стратегий.

Если игрок имеет конечное число m чистых стратегий, смешанная стратегия представляет собой m-мерный вектор 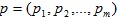, удовлетворяющий условиям: .

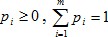Применение смешанных стратегий игрока превращает процесс игры в некоторое случайное испытание, исходами которого являются ситуации игры.

Теорема о максимине.

“Всякая игра двух лиц с нулевой суммой, в которой разрешаются смешанные стратегии, имеет точку равновесия”.

Каждая конечная игра имеет свою цену: .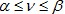

Если один из игроков придерживается своей оптимальной смешанной стратегии 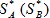, то выигрыш остается неизменным и равным цене игры v независимо от того, что делает другой игрок, если только он не выходит за пределы своих “полезных” стратегий.