6. Детерминированные, стохастические задачи

X - множество рассматриваемых альтернатив, Y - множество возможных исходов.

Предполагается существование причинной связи между выбором некоторой альтернативы 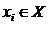 и наступлением соответствующего исхода.

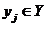Детерминированные задачи принятия решений.

Связь альтернативы с исходом – детерминированная, альтернатива приводит к единственному результату: существует однозначное отображение 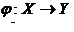, что .

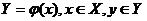Цели и ограничения формально определяются в виде целевых функций и неравенств (равенств). Критерий выбора определяется минимумом целевой функции. Это позволяет построить формальную математическую модель задачи принятия решений и алгоритмически найти оптимальное решение.

Стохастические задачи принятия решений.

Связь альтернативы с исходами – вероятностная (выбор Х определяет некоторую плотность распределения вероятностей на множестве Y).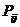- вероятность наступления исхода Y-j, при выборе альтернативы X-i, такого, что  .

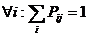Принятие решений в условиях вероятностной определенности базируется на теории статистических решений. В этой теории неполнота и недостоверность информации в реальных задачах учитываются путем рассмотрения случайных событий и процессов. Их вероятностные характеристики являются неслучайными, поэтому с ними можно производить операции по нахождению оптимального решения так же, как с детерминированными характеристиками.

Задачи принятие решений в условиях неопределенности.

Связь альтернативы с исходами имеется, но информация вероятностного характера отсутствует.

Для задач характерны неполнота и недостоверность информации, многообразие и сложность влияния социальных, экономических, политических и технических факторов. Эти обстоятельства не позволяют, по крайней мере, в настоящее время, построит адекватные математические модели решения задач по определению оптимального решения.

Виды неопределенности

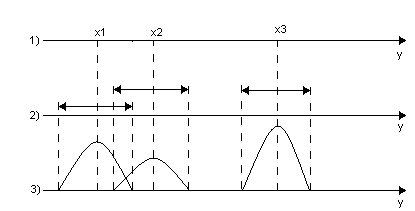
1) Детерминированная задача 

2) Задача в условиях неопределенности 

3) Стохастическая задача